计算机图形学

概论

评分

Lab: 30%
Project: 40%
小测，作业，课堂问答 30%

定义

用像素来表示真实世界的科学技术?
在计算机中建模，处理和显示物体的科学技术。

基本任务

为世界建模
仿真现实世界中物体的行为
显示世界图形与物理学是实现这些任务的传统工具。

为世界建模

对世界的数字表达有很多：

Digital Images 数字图像
3D Geometric Objects 3D 几何图形
Symbolic Descriptions 符号表达

Digital Images 数字图像

优点：直观，容易获取(如拍照)，适合表现复杂细节

缺点：数据量大，不易编辑，分辨率受限，视角固定

3D Geometric Objects 3D 几何图形

优点：数据量小，易于编辑和变换，可从任意视角观察

缺点：难以表现复杂纹理和细节，建模复杂

Symbolic Descriptions 符号表达

优点：数据量最小，完全参数化，精确控制

缺点：表达能力有限，不直观，仅适用于特定场景

我们注重 Graphics Representation。

Point3D {
  double x;
  double y;
  double z;
};
Line {
  Point3D a;
  Point3D b;
};
Cuboid {
  LCS3D local;  // 局部坐标系，其实就是一个点
  double x;
  double y;
  double z;
};

对于复杂的物体，我们往往使用很多的面片来表示它。

Three very important and rather complex attributes:

complex shape
visual look or appearance due to lighting effects
dynamic behaviour due to interaction with other elements of the world — movement, sound, elastic effects…

仿真现实世界中物体的行为

略

显示世界

将三维对象转换成图像（Display,rendering）。

应用

CAD（Computer-Aided Design，计算机辅助设计）：利用计算机进行产品、建筑、机械等的设计、绘图和建模，提高设计效率和精度，常用于工程、建筑、制造等领域。
GIS（Geographic Information System，地理信息系统）：用于采集、存储、管理、分析和展示地理空间数据的系统，广泛应用于地图制作、城市规划、资源管理、环境监测等领域。
影视
游戏
科学可视化
虚拟现实
UI

2D 图形算法

Rasterization 光栅化

绘制一个对象到屏幕上可以归结成两步：

确定屏幕上要画哪些像素点
确定每一个像素点要画成什么颜色

其中的第一个步骤被称为 Rasterization 或 scan conversion。

譬如说，将一条线转化成像素点：

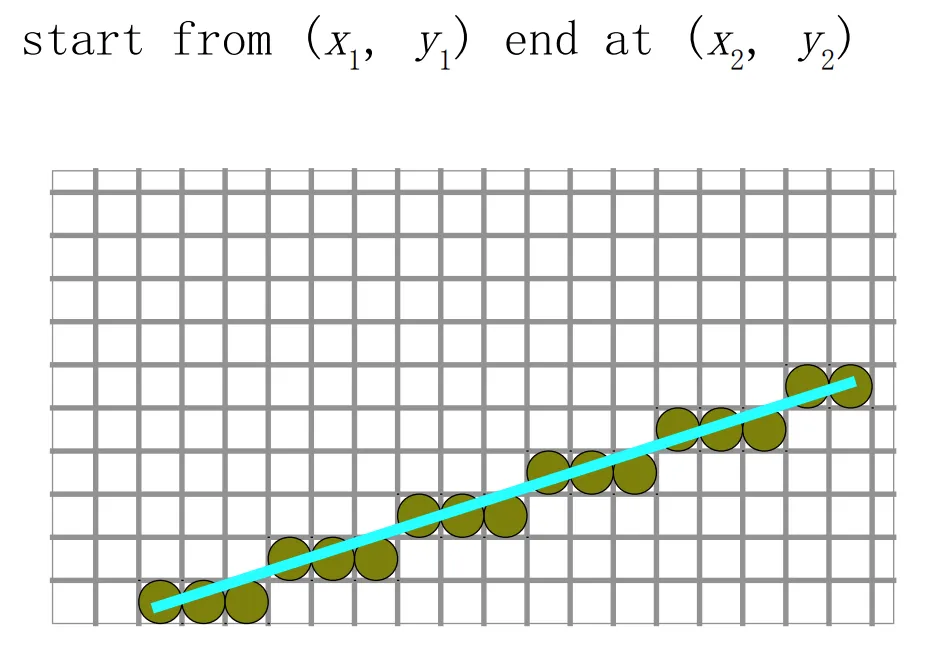
alt text

选择的像素点要尽可能靠近理想直线，同时这个操作性能要好。

DDA 算法

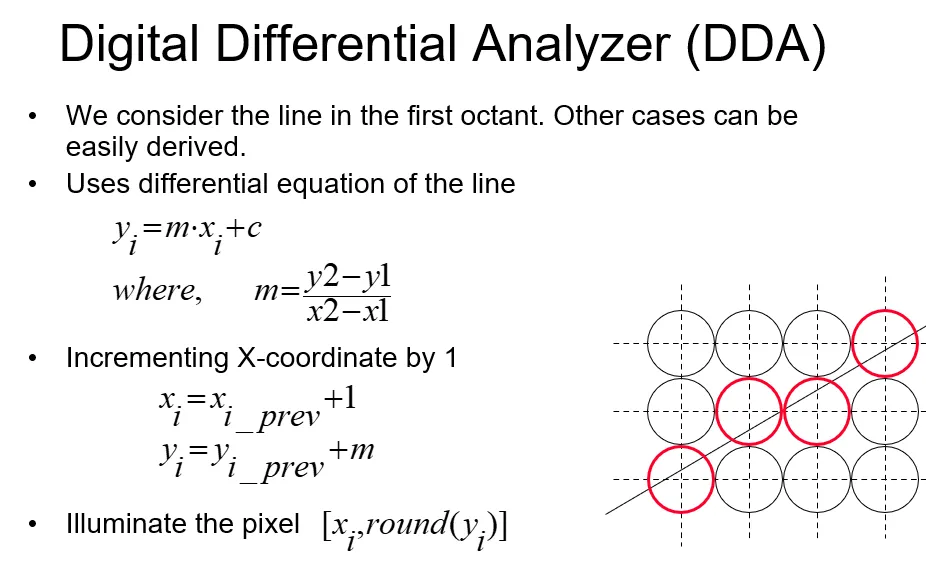
alt text

DDA 算法在上一步的基础上计算下一步，从而减小开销。当然，这里要注意，当 m<1 时，我们应该改为 y+=1, x+=1/m。

这种在上一步的基础上计算下一步的加速方法被称为增量算法 Incremental Algorithm。在使用增量算法时，我们应该注意误差的累加问题。

BLD 算法 Bresenham’s Line Drawing Algorithm

Bresenham 算法是一种高效的整数增量算法，用于在像素网格上绘制直线。我们接下来只讨论直线的斜率绝对值小于 $1$ 的情况。

首先，我们确定直线的起点坐标和终点坐标 $(x_0,y_0),(x_n,y_n)$ 。需要注意的是，这里的坐标都是整数，而非小数。

我们一个个绘制像素点。假设当前已经绘制的最新像素点为 $(x_k,y_k)$ ，下一个点为 $(x_{k+1},y_{k+1})$ ，则有

\begin{align*} x_{k+1}&=x_k+1\\ y_{k+1}&=y_k\text{ or }y_k+1 \end{align*}

我们考虑直线的一般式（这么做可以避免浮点数的引入！）

(y_0-y_n)x+(x_n-x_0)y+x_0y_n-x_ny_0=0

我们可以通过判断直线和 $(x_{k+1},y_{k}+\frac{1}{2})$ 的关系来判断下一个点的 $y$ 是否应该增加。于是，我们定义决策变量

d_k=F(x_{k+1},y_{k}+\frac{1}{2})

如果 $d_k<=0$ ，说明直线在点的上面， $y_{k+1}=y_k+1$ ，反之则 $y_{k+1}=y_k$ 。

这里，我们采用增量算法的思想，发现

d_{k+1}-d_k=A+B(y_{k+1}-y_k)\Rightarrow d_{k+1}=d_k+(y_0-y_n)+(x_n-x_0)(y_{k+1}-y_k)

不妨记

\left\{ \begin{align*} \Delta x &= x_n-x_0\\ \Delta y &= y_n-y_0 \end{align*} \right.

则有

\left\{ \begin{align*} d_{k+1}&=d_k+\Delta x(y_{k+1}-y_k)-\Delta y\\ d_0&=(y_0-y_n)(x_0+1)+(x_n-x_0) \left(y_0+\frac{1}{2}\right)+x_0y_n-x_ny_0\\ &=\frac{1}{2}\Delta x - \Delta y \end{align*} \right.

为了避免引入浮点数，我们重新记 $D_k=2d_k$ ，于是即有：

\left\{ \begin{align*} D_0&=\Delta x - 2 \Delta y\\ D_k>0&:D_{k+1}=D_k- 2 \Delta y,y_{k+1}=y_k\\ D_k\le 0&:D_{k+1}=D_k - 2 \Delta y + 2 \Delta x,y_{k+1}=y_k+1 \end{align*} \right.

当直线斜率大于 1 时，则以 $y$ 为主变量，每次递增 $y$ 。

Bresenham 算法的核心思想就是用一个决策变量跟踪理想直线与像素点的偏差，逐步逼近理想直线。

Polygon Filling

给定一个多边形，找到多边形内部全部的点
任给一个点，判断点是否在多边形内部

Even-Odd Test

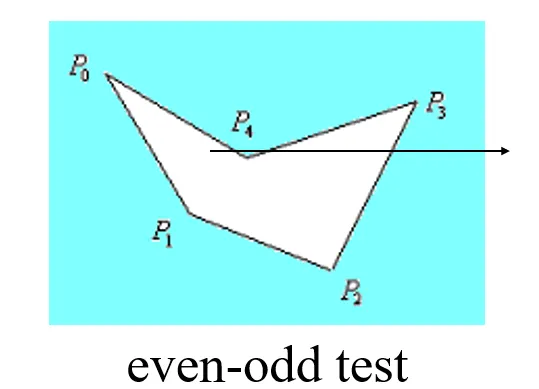
alt text

过点引一条射线，如果和多边形有奇数个交点，那么就在多边形内部，反之在多边形外部。

在计算机图形学中，我们往往希望回避求交问题。

可以将多边形的所有边收集起来，先做一条水平线和这些边求交点。把交点作为一个数组存储，可以发现，第一个交点的左侧为外，右侧为里，如此有一个奇偶状态的不断翻转。因此，我们可以通过点的 $x$ 范围来确定点的奇偶性了。

如果 $y$ 不相同，则可以通过直线斜率找到新的 $y$ 时水平线和直线的交点，然后用类似方法处理。

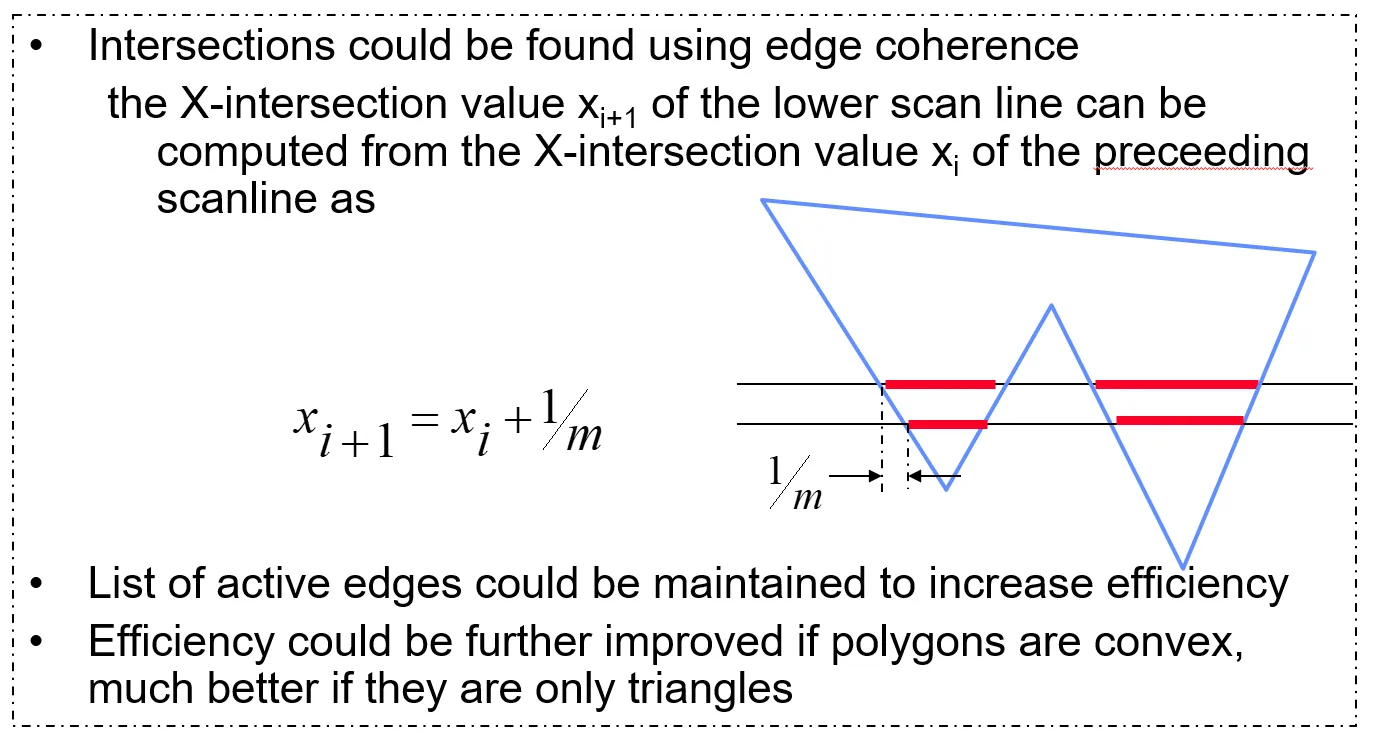
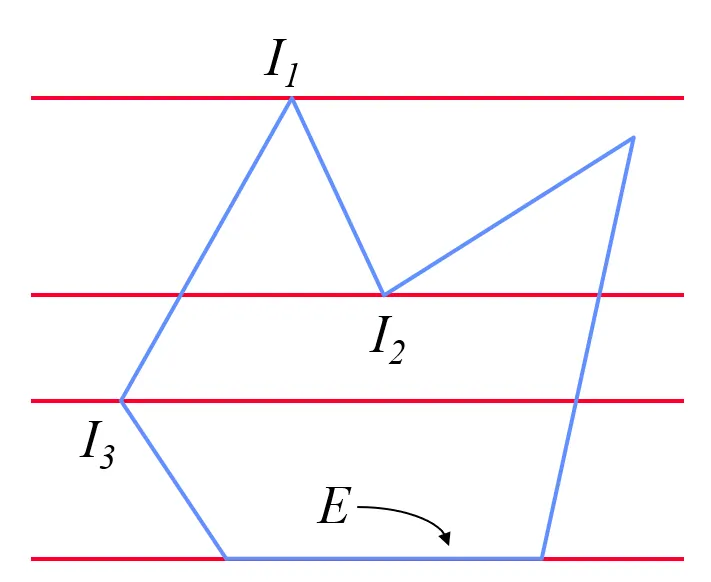
alt text

如果非常巧的，做的直线直接过了边界的转折处且两边界一往上一往下，需要把两边的交点看成两个位置重复的点，而非同一个点（ $I_1,I_2$ ）。

然而如果你关注 $I_3$ ，就会发现我们本应只把他当成一个点，却因为我们关注的是每个边，被处理成了两个点，这样就导致了错误。

同样地，一条平行边可能导致无限多个交点。

alt text

Winding Number Test

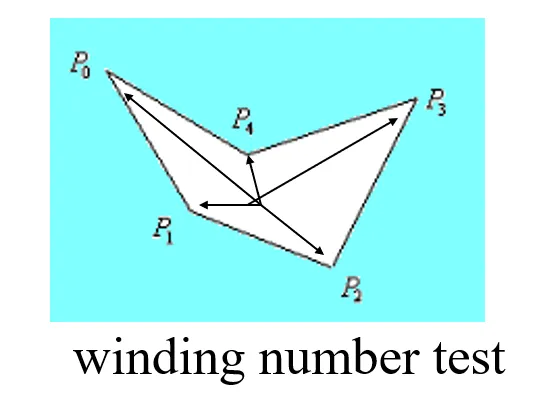
alt text

对于待判定的点 $Q$ ，遍历多边形的每一个顶点 $P_1,\ldots P_n$ ，将从 $Q$ 指向 $P_i,P_{i+1}$ 的两个向量之间的夹角 $\theta_i$ 相加起来。

如果 $Q$ 在多边形外部，则总角度为 $0$ ，反之则为 $\pm 2\pi$ 。